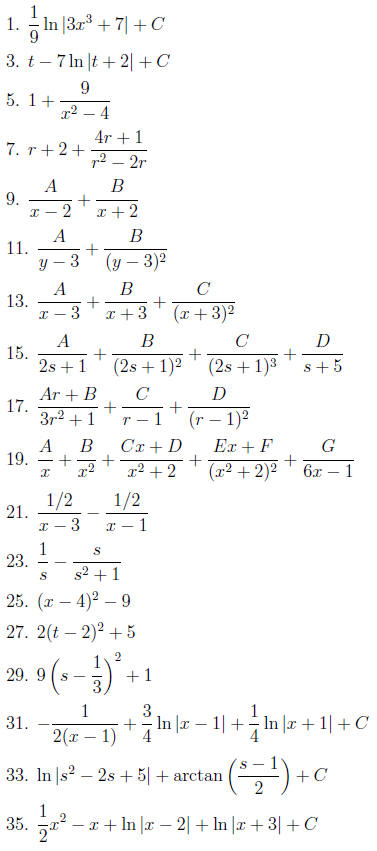Integrals of Rational Functions
5 Completing the Square
In dealing with quadratic factors, it is often useful to rewrite them in a form
which does
not explicitly involve a linear (x) term. To illustrate this process of
completing the square,
consider the polynomial
x2 − 6x + 8.
Take the coefficient of x, divide it by two, and square it to get (−6/2)2
= 32 = 9. Add and
subtract this number and factor the result to get
x2 − 6x + (9 − 9) + 8 = (x2 − 6x + 9) − 1 = (x − 3)2
− 1.
Thus, we have rewritten the original quadratic in a form which lacks a linear
term.
If the coefficient of the x2 term isn’t 1, we must factor it out
before starting. The following
two examples show how to do this.
Example 7: Complete the square for 21 − 4s − s2.
Solution: We start by factoring out the coefficient −1 of s2, and
then add and subtract
(4/2)2 = 4:
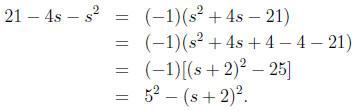
Example 8: Complete the square for 5y2 − 10y +
9.
Solution: Again, we start by factoring out the coefficient 5 of y2;
this time it doesn’t factor
out of the constant term nicely, so we’ll leave the constant term hanging (but
be careful to
add and subtract in the same place—inside the parentheses):
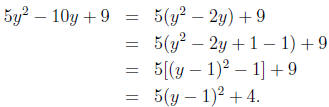
6 Term by Term Integration
In the previous sections we have described how to write any rational function as
the sum
of a polynomial and a partial fraction expansion. To find the integral in this
form, we can
integrate term by term. The integral of a polynomial is easy, and the integral
of a proper
rational function with a linear denominator is easy, too:
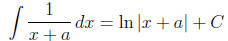
(by substitution, as discussed in section 2). For
integrals with quadratics in the denominator,
the main tool is the formula
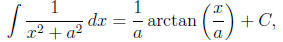
which comes from the basic integration formula
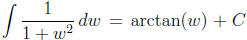using the
substitution w = x/a. If the quadratic involves a linear term, we can first
eliminate it by
completing the square.
Example 9: Find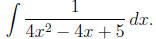 
Solution: The denominator is an irreducible quadratic (try the quadratic
formula—there are
no real roots). Thus, we cannot further break down the integrand using partial
fractions.
To convert it to a form we can integrate, we first complete the square.
Factoring out the
coefficient of x2 and adding and subtracting (−1/2)2 = 1/4
gives
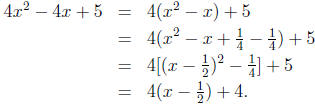
We can then do the integral using the substitution
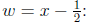
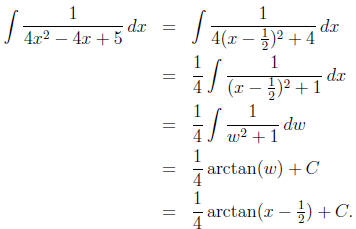
If the denominator is quadratic and the numerator is
linear, adding and subtracting a
constant in the numerator will yield two pieces which can be integrated as
described above.
The key here is to construct a linear term in the numerator which is the
derivative of the
denominator (up to a constant factor).
Example 10: Express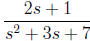 
as
two terms which can be integrated by methods already
considered.
Solution: Since the derivative of the denominator is 2s +
3, we add and subtract 2 in the
numerator to obtain
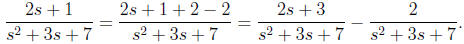
The first of these terms is easily integrated by the
substitution w = s2 + 3s + 7; the second
can be integrated by completing the square and using the formula involving
arctan.
7 Putting It All Together
Having discussed each of the steps separately, now it’s time to put them
together to integrate
rational functions. For our first example, we simply collect the pieces we
worked out in detail
in several previous examples.
Example 11: Find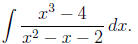 
Solution: Since the integrand is an improper rational
function, we first divide the denominator
into the numerator to obtain
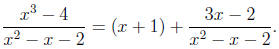
Next, we expand the remaining (proper) rational function using partial fractions:
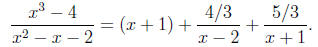
Finally, we integrate term by term:
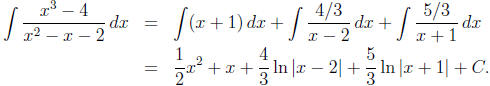
Example 12: Find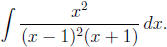 
Solution: Here the integrand is a proper rational function
and the denominator is already
factored, so our first step is to find the partial fraction expansion. This must
take the form
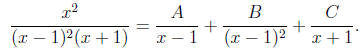
Note that since the factor (x − 1)2 appears
with multiplicity 2, we must include two corresponding
terms in the expansion (the terms involving A and B). Clearing fractions
(multiplying
by the denominator) gives
x2 = (x − 1)(x + 1)A + (x + 1)B + (x − 1)2C.
To find A, B, and C we plug in specific values of x: using x = 1 leads to 1 = 2B
so B = 1/2,
and using x = −1 leads to 1 = 4C so C = 1/4. To find A we could use any other
value of x;
perhaps the easiest one to work with is x = 0, which leads to the equation
0 = −A + B + C.
Plugging in the values B = 1/2 and C = 1/4 we already found leads to A = 3/4.
Substituting
these into the partial fraction expansion gives
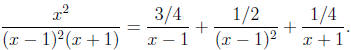
Finally, we integrate term by term:
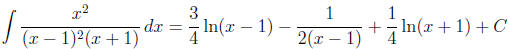
(for the middle integral we used the substitution w = x − 1).
8 Problems
Find the integrals in problems 1–4:
In problems 5–8, express the rational function as the sum
of a polynomial and a proper
rational function.
In problems 9–20, give the correct form of the partial
fraction expansion for the rational
function. Do not evaluate the undetermined coefficients A, B, C, . . . .
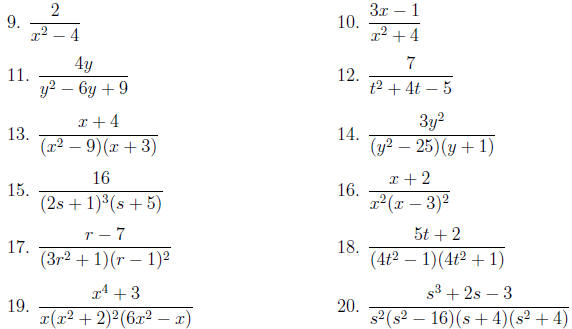
Expand each rational function in problems 21–24 using partial fractions.
Rewrite each polynomial in problems 25–30 by completing the square.
Find the integrals in problems 31–36:
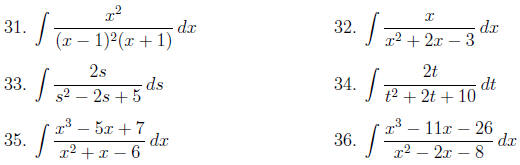
9 Answers to Odd-Numbered Problems
